Расчет параболического отражателя

Enter the parabola dimensions – Введите размеры параболы
Both dimensions must use the same units (integral only) – Оба значения должны быть в одних и тех же единицах измерения (только целые)
Diameter – Диаметр
Depth – Глубина
Focal Point –Точка фокуса

Об этой программе
Эта бесплатная программа была написана, чтобы помочь Вам в разработке солнечного коллектора или WiFi проектов с использованием параболических рефлекторов (отражателей). Для улучшения силы сигнала вашей Wi-Fi антенны или проектирования спутниковой антенны, эта программа позволит рассчитать фокусное расстояние и (х, у) координаты параболы любого диаметра и глубины. С ее помощью можно определить, какой размер и форма необходимые, чтобы сделать вашу параболу очень быстро. Версия 2 включает в себя Wi-Fi расчеты для центрального или смещенного облучателя тарелки. Если вы хотите модифицировать программу, чтобы сделать ее более полезной для вас или послать обратный ответ, вы можете написать мне здесь.

Признательность
Спасибо Франку Шиндлеру, так как для кода подгонки кривой использовалась эта программа, вы можете увидеть его страницу здесь.
Спасибо Бернхарду С. Мюллер за помощь в разработке и бета-тестированию версии 1, вы можете увидеть его сайт здесь.
Спасибо Эдишеру Гиоргадзе за помощь в разработке и бета-тестированию версии 2, вы можете увидеть его страницу здесь.
Cпасибо Полу Уэйду за обеспечение WiFi текстов, расчетов и кодов, они были скопированы непосредственно с его hdl_ant программы, вы можете посетить его сайт и скачать его программу здесь.

Скачать программу
Эта программа была написана на Visual Basic 6, и должна работать на Windows 95 или версиях, вышедших позже. Программа будет работать на Linux с помощью Wine, если вы копируете зависимости файлов в папке, где находится программа. Программа требует файлы времени Visual Basic 6, на вашем компьютере, возможно, они уже установлены. Я бы попытаться загрузить сначала файл меньшего размера (только программу) и посмотреть работает ли она. Если нет, удалите его и загрузить установщик Windows для выполнения стандартной установки Windows.
– Скачать Parabola.exe (137 Кб) (только программа, не включает в себя файлы Visual Basic)
– Скачать Windows Installer (1,65 МБ) (запустите файл Setup.exe для выполнения стандартной установки Windows)
– Скачать VB6 Source Code (155 Кб)
– Скачать VB6 файлы для Linux Wine (740 Кб)

Далее на англоязычной оригинальной странице идет блок ссылок, здесь не отображенный.

Инструкция

1. При запуске программы на экране появится главное окно, показанное на рисунке. Используйте любые единицы, какие хотите, главное, чтобы использовались одни и те же единицы измерения, как для глубины, так и для диаметра. Вы также можете выбрать диаметр и f / D на входе используйте Функции > Выбрать меню (Options > Select Inputs) . Я рекомендую использовать более мелкие единицы измерения: дюймы вместо футов или миллиметры вместо метров, чтобы увеличить разрешение вашего измерений.

2. После ввода некоторых чисел в ячейки Диаметр и Глубина и нажмите кнопку Рассчитать (Calculate), программа покажет вам, сведенную к определенному масштабу форму параболы, которую вы описали, и рассчитает (х, у) координаты кривой параболы на 16 отрезках прямой линии. Вы можете рассчитать координаты (х, у), используя от 2 до 1000 сегментов.

Focal length – длина фокуса
Liner Diameter – линейный диаметр
Segments – отрезки
Volume – объем
Area – площадь

3. Чтобы понять, как будет выглядеть форма и фокусное расстояние, когда глубина увеличивается до 18, удерживаем горизонтальную полосу прокрутки рядом с текстовым полем и наблюдаем за изменением формы параболы.

4. Если нажать кнопку Сохранить текст файла (Save To Text File) , то программа предложит выбрать папку и ввести имя файла, а затем записывает файл с информацией, которую вы видите в текстовом поле справа. Вот как выглядит сохраненный файл при открытии с помощью программы Блокнот (с использованием Lucida Console (вид шрифта) получается непропорционально, где все символы имеют одинаковую ширину, поэтому линия колонны вертикальна). Программа автоматически предложит имя файла, которое включает в себя глубину и диаметр, но вы можете ввести любое имя файла, которое вам нравится.

5. Если бы вы хотели видеть коэффициенты уравнения, которые описывают текущую Параболу, используйте пункт меню Файл > Просмотр коэффициентов (File > View the Coefficients) . Вы увидите окно, подобное этому, которое показывает вам значения, используемые для уравнения параболы:

Уравнение для параболы:
у = а(х^2) + b(x) + c
Коэффициенты, описывающие данную параболу:
Значения примера на скриншоте
Уравнение для данной параболы:
Значения примера на скриншоте

6. Если вы переместите курсор на изображение параболы, то вы увидите отдельные точки, которые рассчитываются программой: координаты (х, у) отображаются в нижней части дисплея. Точка (по горизонтали) ближе всего к курсору мыши, показанная ниже, вы можете видеть местоположение каждой точки, перечисленные в текстовом поле.

7. Есть несколько форматов файлов, которые можно использовать для сохранения данных, который могут быть прочитаны другими программами, например, ACAD, CorelDraw, или MS Excel. Вы можете увидеть эти пункты в меню Файл (File) . Вы можете распечатать график параболы на принтер, выбрав в меню Печать (Print) .

Вы можете изменить передний план и цвет фона графической Параболы, использовав в меню Параметры (Options) .

8. Wi-fi расчеты для центрального или смещенного облучателя тарелки можно сделать с помощью выбора в меню пункта Wi-Fi Расчеты (Wifi Calculations) .

Далее перевод текста со скриншота выше
Inputs – входные данные
Enter Frequency – введенная частота
Enter Diameter – введенный диаметр
Enter Depth – введенная глубина
Select Units – выбранная единица измерения
Illumination angle for feed – Угол освещения
Degree – градус
Space attenuation – протяженность ослабления
Desired taper – Желаемый уклон
Edge – угол
A simple feedhorn would have a diameter of 2.64 wave lenghts for a 3 dB beam width of 24.98 degrees – Простой излучатель имеет диаметр 2.64 длиной волны для ширины луча 3 дБ 24.98 градусов
Gain at 50% efficiency = 14.78 dBi – Усиление эффективности на 50% = 14.78 дБи

Далее перевод текста со скриншота выше
Diameter of large axis of dish – Диаметр большой оси тарелки
Diameter of small axis of dish – Диаметр малой оси тарелки
Depth of dish at deepest pt – Глубина тарелки самой глубокой точке касания
Distance of deepest pt from bottom edge along large axis – Расстояние самой глубокой точки касания от нижнего края вдоль большой оси.
Длина фокуса 780.21 мм
Смещение отражателя является частью полной параболы с диаметром 1912,27 мм, вершина которой находится в нижний край смещения отражателя. Полная парабола имеет f/ D = 0.41, которая определяет критичность местной длины.
Точка фокуса тарелки – это 780.21 мм от нижнего края рефлектора и 1073.14 мм от верхнего края рефлектора.
Для работы с главным лучом на горизонте с питанием на дне, тарелка должна быть наклонена, поэтому большая ось составляет 72.97 градусов выше горизонта.
Угол освещения для питания = 63.00 градусов на большой оси и 60.46 градусов на малой оси. Облучатель с шириной волны 3 дБ необходим 34.18 градусов, что эквивалентно питанию обычной антенны с f/D = 0.94
Усиление 50% эффективности = 38.06 дБи. Если вы все хорошо, то вы можете получить60% усиления эффективности = 38.86 дБи

9. Если вы хотите узнать больше о солнечных коллекторах и проектах солнечных плит, или о математических расчетах параболы, откройте меню и выберите: Файл> Парабола и Сайты солнечного проекта (File > Parabola and Solar Project Websites). Нажмите на веб-сайт и он будет автоматически загружаться в ваш веб-браузер по умолчанию. Нажмите кнопку Скрыть (Hide) , чтобы просмотреть основную форму программы еще раз, когда закончите с веб-сайтом. Коллекцию этих ссылок можно найти здесь.

Этот материал подготовен на основе перевода англоязычной страницы.

R190449733270, Z695426691627 – номера кошельков Webmoney в поддержку развития солнечной и другой подобной энергетики (вопросы можно задать через форум).

Исходные данные к проекту и требования к его содержанию

В задании на проектирование указываются следующие характеристики антенн:

Рабочая длина волны λ .

Ширина главного лепестка диаграммы направленности антенны по уровню половинной мощности 2θ0.5.

Вид облучателя и его основные параметры.

Должны быть определены:

размеры и диаграмма направленности облучателя;

уровень согласования облучателя с питающей фидерной линией;

геометрические параметры параболического рефлектора;

диаграмма направленности и коэффициент усиления антенны;

технические допуски на изготовление рефлектора и смещение облучателя из фокуса.

В ряде случаев в конструкции антенны должны быть предусмотрены меры по устранению воздействия на облучатель волны, отражённой от рефлектора, и расчет облегчённой конструкции рефлектора.

Исходные данные к курсовому проекту:

Рабочая длина волны λ=3,5 [см]

Ширина главного лепестка диаграммы направленности антенны 2ΔθЕ=

Вид облучателя – щелевой.

Тип фидерной линии – волновод.

Введение.

Основными элементами параболической антенны являются металлический отражатель (рефлектор), имеющий форму одной из параболических поверхностей (параболоид вращения, параболический цилиндр и др.), облучатель, помещённый в фокусе такой поверхности, и фидер, питающий облучатель. Применение параболических поверхностей объясняется тем, что в силу своих геометрических свойств они создают синфазное поле в раскрыве рефлектора.

Так как фокусное расстояние любой параболической поверхности является ее геометрическим параметром и выбор его, как правило, не связан с рабочей длиной волны, поле в раскрыве антенны остается синфазным независимо от длины волны. Поэтому параболическая антенна относится к широкодиапазонным антеннам. Практически ее диапазонность ограничивается требованиями к степени согласования облучателя с питающим фидером и пределами допустимых значений ширины главного лепестка диаграммы направленности антенны, которая меняется прямо пропорционально длине волны.

3.2 Облучатели параболических антенн.

В качестве облучателей зеркал, выполненных в виде параболоидов вращения, применяются слабонаправленные антенны, излучающие в сторону зеркала. Фазовый центр облучателя совмещается с фокусом зеркала. Основной поток излучателя должен быть сосредоточен в пределах поверхности облучаемого зеркала так, чтобы напряженность поля на краях зеркала составляла ≈0,3 максимального значения (на оси параболоида). Кроме этого облучатель должен иметь малый "теневой эффект" и должен быть хорошо согласован с питающим его фидером. Коэффициент бегущей волны в фидере не должен быть менее 0,8 в рабочем диапазоне частот. Необходимо также обеспечить достаточную жесткость конструкции облучателя и его защиту от воздействия метеоусловий.

4.Расчет размеров и диаграммы направленности щелевого облучателя.

Щелевой облучатель (облучатель Катлера) представляет собой Т-образный прямоугольный волновод (рис. 4.1), закрытый на концах и имеющий на крыльях в широкой стенке две щели, обращенные к параболоиду и расположенные симметрично относительно питающего волновода. Для герметизации щели закрываются полистироловыми или слюдяными пластинками.

Рис.4.1 Волноводно-щелевой облучатель (облучатель Катлера).

Такие облучатели применяются в коротковолновой части сантиметрового диапазона λ=(2 – 5) см, где конструкция получается компактной, а создаваемы теневой эффект незначителен. Фазовый фронт, создаваемый таким облучателем, близок к сферическому.

Ширина щели принимается равной:

Резонансная длина щели с учетом эффекта укорочения выбирается равной:

Расстояние от укороченного конца волновода до оси щели должно быть равно:

где Λ – длина волны в волноводе, определяется из формулы:

При этом щель оказывается в пучности стоячей волны тока, что обеспечивает максимальную интенсивность излучения.

Для согласования входного сопротивление щели с волновым сопротивлением волновода должно удовлетворяться условие:

Из которого, задаваясь величиной широкой стенки волновода a=0,72λ=2,52 см определяется необходимый размер узкой стенки b1=0,36∙λ=1,02 см.

Расстояние между щелями выбирается равным:

При этом ширина главного лепестка диаграммы направленности облучателя в плоскостях E и H примерно одинакова (плоскость E параллельна узким стенкам питающего волновода). Фазовый центр излучения находится посередине между щелями в плоскости симметрии облучателя. Его совмещают с фокусом отражателя.

Диаграммы направленности облучателя в E и H плоскостях рассчитываются по формулам:

Где θ и ϕ- углы, отсчитываемые в E и H плоскостях от направления к вершине параболического рефлектора.

Обратным излучением щелевого облучателя можно пренебречь и рассматривать диаграммы в пределах изменения угла -90°

Размеры питающего прямоугольного волновода оценивают по условию одноволнового режима для волны H₁₀:

И выбирают стандартный волновод.

Для лучшего согласования и уменьшения влияния внешних поверхностей питающего волновода на поле облучателя питающий волновод сужается вблизи облучателя по узкой стенке до размера b≤0,3a≤0,735 см на длине порядка Λ.

Для возможности регулировки входной реактивности облучателя предусматривается настроечный винт, который помещается в середине Т-образного разветвления.

Прямоугольный волновод, рекомендуемый международной электротехнической комиссией (МЭК)

Обозначение типа	Диапазон,ГГц	a,мм	b,мм	Частота,ГГц	Затухание,дБ/м
от	До
Р100	8,20	12,50	22,9	10,2	9,84	0,11000

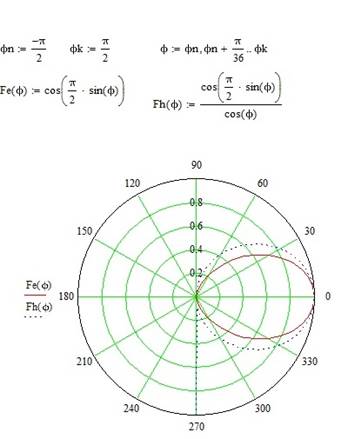
Рис 4.2 Диаграмма направленности облучателя в плоскостях Е и Н в полярной системе координат.

Рис 4.3 Диаграмма направленности облучателя в плоскости E и H

Угол 2θ определяется как угол раствора диаграммы направленности облучателя по уровню 0,3 от максимума поля и его следует определять по более узкой ДН, в данном случае в Е-плоскости:

5.Расчет основных характеристик параболической антенны.

В большинстве случаев зеркальные антенны рассчитываются приближенными методами. При этом характеристики реальных антенн будут несколько отличаться от рассчитанных из-за различия диаграмм направленности реальных и идеальных облучателей, теневого эффекта облучателя, неточности изготовления антенны т. п. Для получения достаточно высоких показателей проектируемой антенны должны быть предусмотрены специальные меры, например: боковые лепестки диаграммы направленности облучателя должны лежать вне области освещения зеркала; фокусное расстояние должно быть скорректировано для фазировки обратного излучения облучателя с полем антенны; необходимо наложить определенные условия на точность изготовления антенны и т. д. С учетом этих замечаний составим следующий порядок расчета антенны с рефлектором в виде параболоида вращения.

1.Для определения геометрических размеров параболической зеркальной антенны (рис 5.1) рассчитаем отношение радиуса раскрыва параболоида R0 к фокусному расстоянию f по формуле:

где θ0 – угол раскрыва параболоида, определяемый как угол раствора диаграммы направленности облучателя по уровню 0.3 от максимума поля в направлении вершины параболоида , что соответствует 0.1 по мощности. В целях большей равномерности облучения параболического рефлектора угол 2θ0 определяем по более узкой ДН облучателя (в Е плоскости). Из диаграммы направленности облучателя получаем 2θ0 =108°.

Рис 5.1 Основные геометрические параметры параболической антенны.

Найденному отношению соответствуют значения коэффициентов K_E=1,17и K_H=1.08.

2.По заданной ширине главного лепестка диаграммы направленности всей антенны в Е-плоскости 2∆θЕ=2,8 0 =0.0489 рад. и по полученным из таблицы K_E =1.17 и K_H =1.08 определяем радиус раскрыва параболоида R из соотношения:

3.По найденным значениям R0 и θ0 рассчитывается фокусное расстояние f.

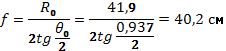
Значение фокусного расстояния должно быть уточнено, если в направлении заднего лепестка ДН облучателя поле противофазно полю главного лепестка (рупорные, щелевые облучатели), фокусное расстояние должно удовлетворять соотношению:

В результате при n=23 получаем уточненное фокусное расстояние:

Для полученных значений R и f рассчитывается профиль параболического отражателя из геометрической зависимости:

и глубина зеркала = 10,9 см.

4.Для расчета функций направленности проводится вначале расчет амплитудного распределения поля в раскрыве (апертуре) антенны.

Для упрощения расчета ДН антенны истинное амплитудное распределение поля аппроксимируют некоторой функцией, например, степенным рядом, в котором учитываются три члена:

Где 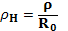– нормированное расстояние произвольной точки раскрыва от его центра: 0≤ρ_H≤1; – постоянные коэффициенты.

Вначале рассчитывают истинное распределение амплитуды fист(ρ_Н), связанное с нормированной функцией направленности облучателя F(θ) соотношением:

где ρ_H=

θ=2arctg

Изменяя ρ_Н от 0 до 1 с шагом 0.1 находят соответствующие значения θ, рассчитывают F(θ) по формулам или графикам диаграммы облучателя, умножают на соответствующие значения множителя (1+cos⁡θ)/2 и составляют таблицу зависимости fист(ρ_Н) и строят график этой функции.

Рис5.2 Истинное распределение амплитуды f_ист(ρ_Н).

Далее необходимо потребовать, чтобы fист(ρ_H) и fаппр(ρ_H) совпадали в двух точках, например, при ρ_Н=0.5 и ρ_Н=1 из таблицы расчетов fист(ρ_H) находим значения fист(0.5)=Δ1, fист(1)= Δ2 и требуем выполнения двух равенств:

в моем случае Δ1=0.94 и Δ2=0.8 тогда:

из решения этой системы находим два неизвестных коэффициента а2 и а4, подставляем их в выражения fаппр(ρH)=1+a2 ρ2H+a4 ρ4H, рассчитываем эту аппроксимирующую функцию при ρH изменяющемся от 0 до1 с шагом 0.1 и строим график аппроксимирующей функции fист(ρH).

Рис 5.3 Аппроксимирующая функция fаппр(ρ_H).

5.Зная распределение поля в раскрыве, рассчитывается диаграмма направленности антенны.

Для амплитудного распределения поля в раскрыве антенны вида степенного трехчлена fаппр(ρ_H) функция направленности имеет вид:

где u=kRsinθ, k=2π/2, Λ_i(u) – лямбда – функция i-го порядка.

Расчет f(θ) проводят, изменяя θ через 0,5÷1 и рассчитывают главный лепесток и два боковых (при этом f(θ) два раза меняет знак).

Θ0	U				F(θ)
0,403
0.5	0,654	0,957	0,979	0,977	0,375	0,930
1,316	0,831	0,866	0,898	0,353	0,875
1.5	1,955	0,648	0,759	0,794	0,252	0,625
2,632	0,377	0,543	0,642	0,170	0,422
2.5	3,309	0,337	0,351	0,479	0,258	0,310
3,910	0,137	0,240	0,344	0,118	0,230
3.5	4,585	-0,108	0,108	0,224	-0,014	-0,034
5,261	-0,132	-0,064	0,112	0,095	0,235
4.5	5,936	-0,105	-0,051	0,034	0,021	-0,052
6,611	-0,032	-0,057	-0,011	0,043	0,106
5,5	7,210	0,010	-0,043	-0,027	0,041	0,102
7,883	0,051	-0,021	-0,029	0,041	0,102
6,5	8,556	0,064	0,002	-0,020	0,034	0,084
9,229	0,047	0,017	-0,008	0,053	0,131
7,5	9,863	0,018	0,029	0,0004	-0,026	-0,064
10,05

Рис 2.7 Диаграмма направленности антенны F_A(θ).

Из графика можно определить, что ширина главного лепестка по уровню 0.7 от максимального равен: 0.02 радиан или 1.35 градуса, что примерно равно заданному значению ширины лепестка диаграммы направленности (2,8 градусf). Уровень первого бокового лепестка равен: 0.129. Уровень второго бокового лепестка равен: 0.061.

Рассчитаем коэффициент усиления антенны:

где S=πR 2 – площадь раскрыва параболоида,

η – коэффициент полезного действия антенны, равный: 0.8,

ν – коэффициент использования поверхности раскрыва параболоида вращения, равный: 0.8.

Расчет облегченной конструкции параболического зеркала.

Для уменьшения веса антенны и ослабления давления ветра на параболическое зеркало его выполняют не сплошным, а из отдельных проводов или пластин, либо перфорируют (рис 6.1).

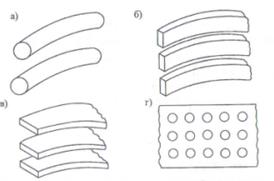
Рис 6.1 Облегченные конструкции отражающей поверхности:

а – параллельные провода; б и в – параллельные пластины;

г – перфорированный лист.

При изготовлении отражающей поверхности из металлических пластин или цилиндрических проводов должны выполняться следующие условия:

а) вектор Е электромагнитной волны должен быть параллелен элементам решетки (пластинам или проводам);

б) расстояние между проводами или пластинами должно быть не более

см.

Перфорированная поверхность представляет собой поверхность из металлического листа с круглыми или овальными отверстиями. Размер отверстия, параллельный вектору E, должен быть меньше . Расстояние между центрами отверстий следует выбирать в пределах .

При выборе параметров рефлектора облегченной конструкции следует исходить из условия: коэффициент пропускания Т, определяемый как отношение мощности волны, прошедшей за зеркало, к мощности падающей на зеркало волны, не должен превосходить Т_доп=0.01. Для параболоида вращения с решетчатой или перфорированной поверхностями имеем: